Countably Semiadditive Functionals and the Hardy–Littlewood Maximal Operator

E. I. Berezhnoj, E. I. Smirnov

Abstract


Abstract: We describe the continuity of nonlinear Hardy–Littlewood maximal operator in nonmetricable function space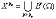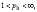,  is a measurable subset of Rn with finite measure.


Keywords


Hardy–Littlewood; Maximal function; Countably semiadditive; Inductive limit of Lebesgue spaces

Full Text:

PDF

References


Kinnunen, J. (1997). The Hardy–Littlewood maximal function of a Sobolev function. Israel J. Math., 100, 117-124.


Lewis, J. (1993). On very weak solutions of certain elliptic systems. Communications in Partial Differential Equations, 18, 1515-1537.


Stein, E. M. (1970). Singular integrals and differentiability properties of functions. Princeton University Press.


Smirnov, E. I. (2002). Hausdorff spectra in functional analysis. London: Springer-Verlag.




DOI: http://dx.doi.org/10.3968/j.sms.1923845220130702.1760

DOI (PDF): http://dx.doi.org/10.3968/g5338

Refbacks

  • There are currently no refbacks.


Copyright (c)



Share us to:   

Reminder

If you have already registered in Journal A and plan to submit article(s) to Journal B, please click the CATEGORIES, or JOURNALS A-Z on the right side of the "HOME".


We only use three mailboxes as follows to deal with issues about paper acceptance, payment and submission of electronic versions of our journals to databases:
[email protected]; [email protected]; [email protected]

 Articles published in Studies in Mathematical Sciences are licensed under Creative Commons Attribution 4.0 (CC-BY).

 STUDIES IN MATHEMATICAL SCIENCES Editorial Office

Address: 1055 Rue Lucien-L'Allier, Unit #772, Montreal, QC H3G 3C4, Canada.

Telephone: 1-514-558 6138

Http://www.cscanada.net
Http://www.cscanada.org
E-mail:[email protected]

Copyright © 2010 Canadian Research & Development Centre of Sciences and Cultures