Countably Semiadditive Functionals and the Hardy–Littlewood Maximal Operator

E. I. Berezhnoj, E. I. Smirnov

Abstract


Abstract: We describe the continuity of nonlinear Hardy–Littlewood maximal operator in nonmetricable function space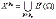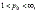,  is a measurable subset of Rn with finite measure.


Keywords


Hardy–Littlewood; Maximal function; Countably semiadditive; Inductive limit of Lebesgue spaces

Full Text:

PDF

References


Kinnunen, J. (1997). The Hardy–Littlewood maximal function of a Sobolev function. Israel J. Math., 100, 117-124.


Lewis, J. (1993). On very weak solutions of certain elliptic systems. Communications in Partial Differential Equations, 18, 1515-1537.


Stein, E. M. (1970). Singular integrals and differentiability properties of functions. Princeton University Press.


Smirnov, E. I. (2002). Hausdorff spectra in functional analysis. London: Springer-Verlag.




DOI: http://dx.doi.org/10.3968/j.sms.1923845220130702.1760

DOI (PDF): http://dx.doi.org/10.3968/g5338

Refbacks

  • There are currently no refbacks.


Copyright (c)



Share us to:   

Please send your manuscripts to [email protected]，or  [email protected]  for consideration. We look forward to receiving your work.

 

 Articles published in Studies in Mathematical Sciences are licensed under Creative Commons Attribution 4.0 (CC-BY).

 STUDIES IN MATHEMATICAL SCIENCES Editorial Office

Address: 1055 Rue Lucien-L'Allier, Unit #772, Montreal, QC H3G 3C4, Canada.

Telephone: 1-514-558 6138

Http://www.cscanada.net
Http://www.cscanada.org
E-mail:[email protected]

Copyright © 2010 Canadian Research & Development Centre of Sciences and Cultures